Fundamento
La perspectiva caballera es la proyección oblicua y cilíndrica (hecha con paralelas) de una figura. Para una buena comprensión de la figura la colocamos de forma que una cara esté paralela (x, z) o coincidente con el plano de cuadro o del dibujo. De esta manera la cara paralela mantiene sus dimensiones y forma inalteradas (homotecia afín), mientras que la proyección de su eje “y” experimenta una reducción (a / b) lo que favorece una apariencia más real de la figura.
Véase que la sombra de rayos paralelos (solar) de la figura con una cara paralela al suelo es la perspectiva caballera de la figura pero con ampliación del tamaño -en este caso por estar el sol en el crepúsculo- en vez de reducción como se viene utilizando en caballera. Las demás caras del cubo: verde, azul, violeta, esto es, las que no son paralelas al plano del cuadro, son afines a su representación o proyección en perspectiva caballera.

Perspectiva caballera del cubo
Aquí observamos la perspectiva caballera del cubo con una cara en verdadera forma y la profundidad del eje y reducido en este caso al 50%. El ángulo se empieza a contar a partir del eje x hacia la derecha, en este caso particular se ha escogido 315º sexagesimales. La pieza por encima de 180º se observa como si se estuviera viendo desde abajo.

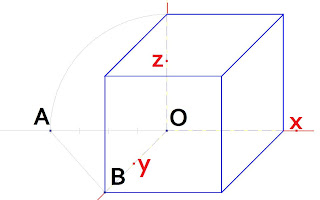
La perspectiva caballera del cubo con una reducción de ¾ sobre el eje y (OA se reduce a OB en relación de 4 a 3).
La perspectiva caballera de una recta m horizontal con sus 3 proyecciones m1 m2 m3.

La perspectiva caballera de un plano oblicuo con sus 3 trazas p1 p2 p3.
Las trazas siempre se cortan en un eje, con lo que si nos dan p. ej., p1 y p3, basta con prolongar p1 hasta que corte al eje x, en el punto de intersección se pasa una recta por la intersección de p3-z y obtenemos p2.

Dos planos oblicuos z p en perspectiva caballera con su recta de intersección I.

Proyección del pentágono regular sobre el plano XOY con la reducción b/a sobre el eje y con un ángulo de 135º.

La perspectiva caballera de uncuadrado ABCD sobre el plano XOY con reducción ¾.

Paraboloide hiperbólico en perspectiva caballera.

La perspectiva caballera de un cilindro y un cono. El hecho de que la perspectiva caballera sea una proyección oblicua hace que las figuras salgan poco reales: el eje mayor de la elipsem (círculo en perspectiva) aparece con cierto ángulo respecto a la horizontal, cosa que no sucede en nuestra percepción visual que la reconoce siempre horizontal.

Pirámide con una cara apoyada en el plano YOZ. La longitud real del círculo de dimensión diametral OP, que inscribe la base de la figura, se reduce a la longitud OB.
BP determina por tanto la dirección de todos los puntos que se reducen sobre el eje y (AB).

La perspectiva caballera de un prisma recto de base hexagonal regular siguiendo los parámetros del ejercicio anterior.

Pieza en perspectiva caballera construida a partir de sus proyecciones diédricas en planta y alzado. El segmento O2 se reduce a OA, longitud que se traslada al eje Z a la dimensión 1. (Por convenio la reducción se aplica sobre el eje y que es el que bascula, en el dibujo z y están intercambiados.)

Pieza Con reducción ½. Para obtener la perspectiva de un punto cualquiera A, se proyecta su proyección A2 en la dirección del eje y A1 en la dirección de reducción 2 es a 1. La intersección de las dos direcciones A2-A y A1-A es la perspectiva del punto.

La perspectiva caballera de una pirámide truncada de base cuadrada a reducción 3/5 y ángulo 45º. El ángulo en la perspectiva caballera siempre se toma en sentido de giro hacia la derecha y empezando a contar a partir del eje x.

La misma figura con una reducción de 2/3 y ángulo de reducción sobre el eje y de 2/3.

Si el punto A está localizado a cierta altura respecto al plano horizontal xy , una vez obtenida la perspectiva de su proyección A’ se levanta una vertical a partir de este punto con la cota en verdadera magnitud, que es la que corresponde al alzado en A2. La intersección de la dirección A-A2 (la del eje y) y de la vertical por A’ localiza al punto A.

La perspectiva caballera de dos prismas superpuestos con una reducción de 2/3 y ángulo de 135º. La longitud MO se reduce a PO sobre el eje y abatido, con lo que en la perspectiva M se transforma en P’. La dirección MP es la que define la reducción sobre el eje y y todos los puntos la siguen, así, N se transforma en N’, etc.


En la figura podemos observar la perspectiva caballera de un cilindro con sus dos proyecciones en planta y alzado, como el ángulo XOY’ es mayor de 180°, en este caso son 215°, la figura se ve como si la observáramos desde abajo. La reducción que se ha aplicado es de un medio.
En la prolongación del eje Z vemos como las dimensiones del cuadrado en planta se proyectan sobre el mismo generando el segmento a, a continuación este segmento se proyecta sobre el eje y’, con la reducción correspondiente. Podemos observar en la planta del cuadrado que por los vértices del mismo hemos hecho paralelas a estas direcciones -en color verde- para obtener sobre la cara XOY’ la proyección en perspectiva caballera de la planta.

En el dibujo observamos la forma de una casa en perspectiva caballera con el ángulo De 135° entre los dos ejes X e Y. El hecho de que la reducción sea ¾, sólo aplicable sobre el eje Y, supone que el segmento a aparece en el dibujo a ¾ de su dimensión real. Tenemos por contra que sobre los otros dos ejes, el horizontal y vertical, las medidas aparecen en verdadera magnitud, sin reducción alguna,- si el dibujo está hecho a escala uno partido uno.

En el dibujo observamos un cubo en perspectiva caballera con la reducción correspondiente y con un ángulo XOY’ de 135°. Se han calculado las sombras que proyecta sobre el suelo y las propias de la figura. Como los rayos del sol son paralelos, en color verde, estamos hablando de luz solar. Para ello se ha indicando la dirección norte-sur, como la dirección de la sombra del segmento vertical es n’, tenemos que el acimut es a, ya que es el ángulo que forma la dirección de la sombra de una vertical y la línea norte-sur hacia la derecha. Mientras que la altitud a la que está el sol, o sea el ángulo que forma respecto a la línea del horizonte es h.
http://calculo-de-sombras.blogspot.com/
http://calculo-de-reflejos.blogspot.com/
http://sombras-en-perspectiva-conica.blogspot.com/
http://reloj-de-sol.blogspot.com/

En el dibujo podemos observar la perspectiva caballera de una pirámide con un ángulo de 45°, como siempre contabilizado a partir del eje X y en el sentido de las agujas del reloj. Como podemos observar también el segmento b en planta correspondiente al lado de la base de la figura en color ocre se transforma en la perspectiva caballera en un segmento reducido a un medio, ya que hemos hecho centro en el origen de coordenadas de los ejes y trasladado el punto medio A mediante un giro sobre el eje y. La altura de la figura está en verdadera magnitud, ya que sobre el eje Z. no se aplica reducción alguna.

La perspectiva militar es un caso particular de la perspectiva caballera en la que la planta de la figura es la que aparece en verdadera forma. Con ello podemos coger el plano de una casa y desplazarlo en una dirección vertical hasta obtener el techo o forjado del piso. Uniendo mediante líneas verticales las dos formas planas correspondientes al suelo y al techo obtenemos la perspectiva Militar de la figura.
Véase que la sombra de rayos paralelos (solar) de la figura con una cara paralela al suelo es la perspectiva caballera de la figura pero con ampliación del tamaño -en este caso por estar el sol en el crepúsculo- en vez de reducción como se viene utilizando en caballera. Las demás caras del cubo: verde, azul, violeta, esto es, las que no son paralelas al plano del cuadro, son afines a su representación o proyección en perspectiva caballera.

Perspectiva caballera del cubo
Aquí observamos la perspectiva caballera del cubo con una cara en verdadera forma y la profundidad del eje y reducido en este caso al 50%. El ángulo se empieza a contar a partir del eje x hacia la derecha, en este caso particular se ha escogido 315º sexagesimales. La pieza por encima de 180º se observa como si se estuviera viendo desde abajo.

La perspectiva caballera del cubo con una reducción de ¾ sobre el eje y (OA se reduce a OB en relación de 4 a 3).

La perspectiva caballera de una recta m horizontal con sus 3 proyecciones m1 m2 m3.

La perspectiva caballera de un plano oblicuo con sus 3 trazas p1 p2 p3.
Las trazas siempre se cortan en un eje, con lo que si nos dan p. ej., p1 y p3, basta con prolongar p1 hasta que corte al eje x, en el punto de intersección se pasa una recta por la intersección de p3-z y obtenemos p2.

Dos planos oblicuos z p en perspectiva caballera con su recta de intersección I.

Proyección del pentágono regular sobre el plano XOY con la reducción b/a sobre el eje y con un ángulo de 135º.

La perspectiva caballera de uncuadrado ABCD sobre el plano XOY con reducción ¾.

Paraboloide hiperbólico en perspectiva caballera.

La perspectiva caballera de un cilindro y un cono. El hecho de que la perspectiva caballera sea una proyección oblicua hace que las figuras salgan poco reales: el eje mayor de la elipsem (círculo en perspectiva) aparece con cierto ángulo respecto a la horizontal, cosa que no sucede en nuestra percepción visual que la reconoce siempre horizontal.

Pirámide con una cara apoyada en el plano YOZ. La longitud real del círculo de dimensión diametral OP, que inscribe la base de la figura, se reduce a la longitud OB.
BP determina por tanto la dirección de todos los puntos que se reducen sobre el eje y (AB).

La perspectiva caballera de un prisma recto de base hexagonal regular siguiendo los parámetros del ejercicio anterior.

Pieza en perspectiva caballera construida a partir de sus proyecciones diédricas en planta y alzado. El segmento O2 se reduce a OA, longitud que se traslada al eje Z a la dimensión 1. (Por convenio la reducción se aplica sobre el eje y que es el que bascula, en el dibujo z y están intercambiados.)

Pieza Con reducción ½. Para obtener la perspectiva de un punto cualquiera A, se proyecta su proyección A2 en la dirección del eje y A1 en la dirección de reducción 2 es a 1. La intersección de las dos direcciones A2-A y A1-A es la perspectiva del punto.

La perspectiva caballera de una pirámide truncada de base cuadrada a reducción 3/5 y ángulo 45º. El ángulo en la perspectiva caballera siempre se toma en sentido de giro hacia la derecha y empezando a contar a partir del eje x.

La misma figura con una reducción de 2/3 y ángulo de reducción sobre el eje y de 2/3.

Si el punto A está localizado a cierta altura respecto al plano horizontal xy , una vez obtenida la perspectiva de su proyección A’ se levanta una vertical a partir de este punto con la cota en verdadera magnitud, que es la que corresponde al alzado en A2. La intersección de la dirección A-A2 (la del eje y) y de la vertical por A’ localiza al punto A.

La perspectiva caballera de dos prismas superpuestos con una reducción de 2/3 y ángulo de 135º. La longitud MO se reduce a PO sobre el eje y abatido, con lo que en la perspectiva M se transforma en P’. La dirección MP es la que define la reducción sobre el eje y y todos los puntos la siguen, así, N se transforma en N’, etc.


En la figura podemos observar la perspectiva caballera de un cilindro con sus dos proyecciones en planta y alzado, como el ángulo XOY’ es mayor de 180°, en este caso son 215°, la figura se ve como si la observáramos desde abajo. La reducción que se ha aplicado es de un medio.
En la prolongación del eje Z vemos como las dimensiones del cuadrado en planta se proyectan sobre el mismo generando el segmento a, a continuación este segmento se proyecta sobre el eje y’, con la reducción correspondiente. Podemos observar en la planta del cuadrado que por los vértices del mismo hemos hecho paralelas a estas direcciones -en color verde- para obtener sobre la cara XOY’ la proyección en perspectiva caballera de la planta.

En el dibujo observamos la forma de una casa en perspectiva caballera con el ángulo De 135° entre los dos ejes X e Y. El hecho de que la reducción sea ¾, sólo aplicable sobre el eje Y, supone que el segmento a aparece en el dibujo a ¾ de su dimensión real. Tenemos por contra que sobre los otros dos ejes, el horizontal y vertical, las medidas aparecen en verdadera magnitud, sin reducción alguna,- si el dibujo está hecho a escala uno partido uno.

En el dibujo observamos un cubo en perspectiva caballera con la reducción correspondiente y con un ángulo XOY’ de 135°. Se han calculado las sombras que proyecta sobre el suelo y las propias de la figura. Como los rayos del sol son paralelos, en color verde, estamos hablando de luz solar. Para ello se ha indicando la dirección norte-sur, como la dirección de la sombra del segmento vertical es n’, tenemos que el acimut es a, ya que es el ángulo que forma la dirección de la sombra de una vertical y la línea norte-sur hacia la derecha. Mientras que la altitud a la que está el sol, o sea el ángulo que forma respecto a la línea del horizonte es h.
http://calculo-de-sombras.blogspot.com/
http://calculo-de-reflejos.blogspot.com/
http://sombras-en-perspectiva-conica.blogspot.com/
http://reloj-de-sol.blogspot.com/

En el dibujo podemos observar la perspectiva caballera de una pirámide con un ángulo de 45°, como siempre contabilizado a partir del eje X y en el sentido de las agujas del reloj. Como podemos observar también el segmento b en planta correspondiente al lado de la base de la figura en color ocre se transforma en la perspectiva caballera en un segmento reducido a un medio, ya que hemos hecho centro en el origen de coordenadas de los ejes y trasladado el punto medio A mediante un giro sobre el eje y. La altura de la figura está en verdadera magnitud, ya que sobre el eje Z. no se aplica reducción alguna.

La perspectiva militar es un caso particular de la perspectiva caballera en la que la planta de la figura es la que aparece en verdadera forma. Con ello podemos coger el plano de una casa y desplazarlo en una dirección vertical hasta obtener el techo o forjado del piso. Uniendo mediante líneas verticales las dos formas planas correspondientes al suelo y al techo obtenemos la perspectiva Militar de la figura.
Teneis algúna solucion a esta prueba?
ResponderEliminarel volumen cúbico esta representado en el sistema de perspectiva caballera, sus medidas son 4x4x4.Dibujarlo en el sistema diedrico, con sus seis vistas en el sistema europeo.
Si es un cubo de 4x4x4 sus vistas diédricas son 6 cuadrados de 4x4 (las 6 caras) colocados correlativamente.
ResponderEliminar